1007. Minimum Domino Rotations For Equal Row

Problem

In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the ith domino.  (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the ith domino, so that A[i] and B[i] swap values.

Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.

If it cannot be done, return -1.

Example 1:

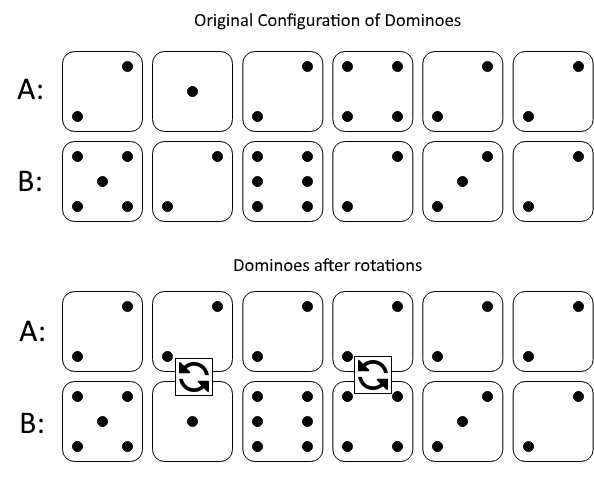
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation:
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation:
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

• 2 <= A.length == B.length <= 2 * 104
• 1 <= A[i], B[i] <= 6

Discussion

Nothing special for this problem. Given two list of dominos of a sized-6-enum, we can easily setup counters for them and perform comparison. We can easily imagine that the solution would be linear.

Solution

Our solution begins with construction of two counters based on the input lists.

Then we can find the most frequent elements among them and decide what list is the dominant one. Afterwards we locate the most frequent element in the dominant list, and perform linear operation on both list.

As long as elements need to be flipped exists, we compare the same index in another list. We then accumulate the number of elements needed to be flipped or return -1 indicating impossibility of dominoes rotation.

from collections import Counter

class Solution:
    def minDominoRotations(self, A: List[int], B: List[int]) -> int:
        counter_a = Counter(A)
        counter_b = Counter(B)

        max_a, max_b = max(counter_a, key=counter_a.get), max(counter_b, key=counter_b.get)
        if counter_a[max_a] >= counter_b[max_b]:
            val, main, aux = max_a, A, B
        else:
            val, main, aux = max_b, B, A

        result = 0

        for i in range(len(main)):
            if main[i] is val:
                continue

            if main[i] is not val and aux[i] is val:
                result += 1

            if main[i] is not val and aux[i] is not val:
                return -1

        return result

Complexity Analysis

• Time Complexity: O(n), as all operations are linear.
• Space Complexity: O(1), as domino is a sized-6-enum, our counter cache is only O(6) == O(1).