1344. Angle Between Hands of a Clock

Problem

Given two numbers, hour and minutes. Return the smaller angle (in degrees) formed between the hour and the minute hand.

Example 1:

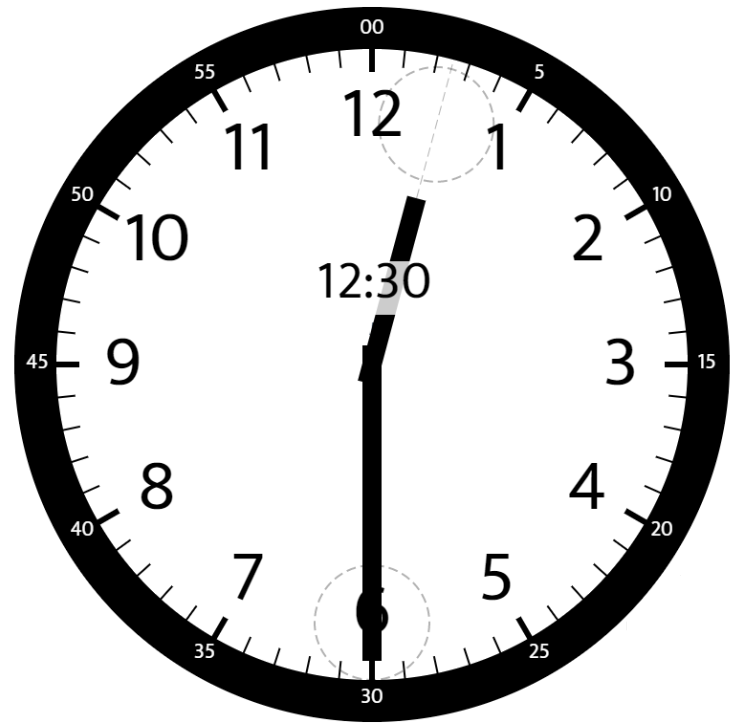
Input: hour = 12, minutes = 30
Output: 165

Example 2:

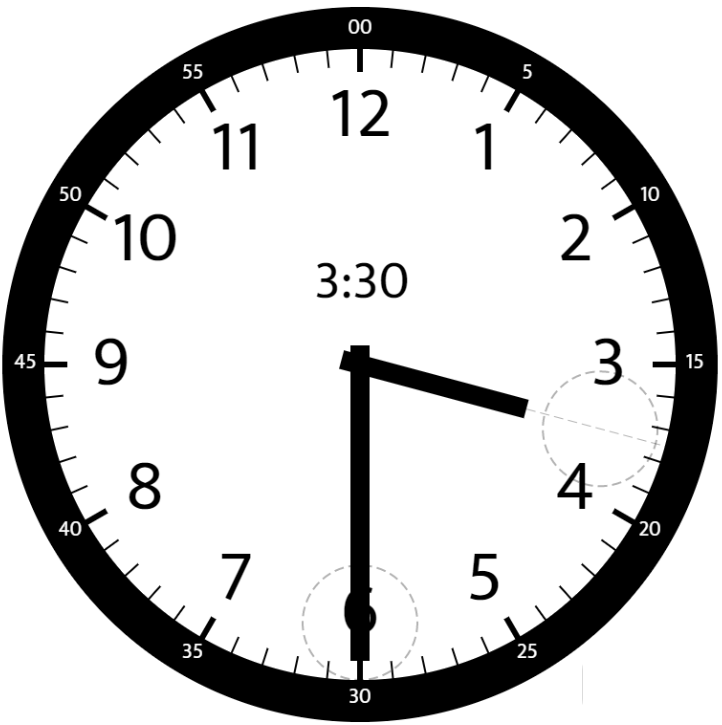
Input: hour = 3, minutes = 30
Output: 75

Example 3:

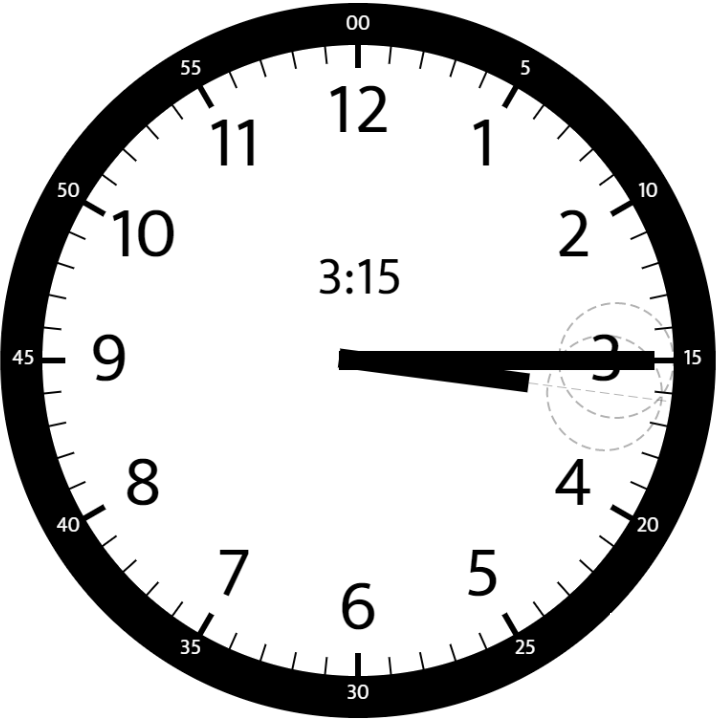
Input: hour = 3, minutes = 15
Output: 7.5

Example 4:

Input: hour = 4, minutes = 50
Output: 155

Example 5:

Input: hour = 12, minutes = 0
Output: 0

Constraints:

• 1 <= hour <= 12
• 0 <= minutes <= 59
• Answers within 10^-5 of the actual value will be accepted as correct.

Discussion

Solving this, we first have the fact that there is 12 hours and 60 minutes on a clock. Thus, degree (from 00:00) of minute would be minutes * (360/60), and degree of hour would be hours * (360/12) + minutes * (360/60/12). Finally we take the absolute value of the degrees' difference.

There are two more tricky points:

1. Consider hours >= 12
2. Consider degree between the two hands always small than 180. Thus we choose the opposite angle when the value > 180.

Solution

Our solution simply evaluates deg_m for minutes and deg_h for hours. We use (hour % 12) to prevent hours larger than 12.

And we take min(result, 360 - result) as the final solution to prevent values larger than 180.

class Solution:
    def angleClock(self, hour: int, minutes: int) -> float:
        deg_m = minutes * 6
        deg_h = (hour % 12)* 30 + minutes * 0.5

        result = abs(deg_h - deg_m)

        return min(result, 360 - result)

Complexity Analysis

• Time Complexity: O(1) as only numeric calculation is involved.
• Space Complexity: O(1) as only numeric calculation is involved.