74. Search a 2D Matrix

Problem

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3
Output: true

Example 2:

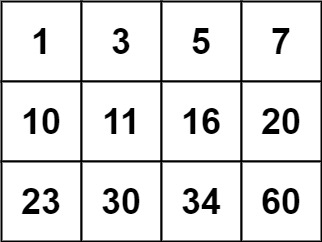
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13
Output: false

Example 3:

Input: matrix = [], target = 0
Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 0 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

Discussion

It's trivial that this problem is modified from the classic binary search problem, with input list becoming 2D-array.

We can imagine the 2D-array to be flatten as an normal array, then the problem is simplified as a binary search problem. Handling the search criteria and evaluation from the 2D-array input and it's done.

Solution

Our problem begins with a classic binary search setup. As the input become 2D-array, we set the tail to be size_i * size_j - 1.

And in each evaluation, we have to project the temporary value mid back to index of the 2D-array as mid // size_j and mid % size_j.

from typing import List

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if not len(matrix) or not matrix[0]: return False

        size_i, size_j = len(matrix), len(matrix[0])
        head, tail = 0, size_i * size_j - 1

        while head < tail:
            mid = (head + tail) // 2

            i, j = mid // size_j, mid % size_j

            value = matrix[i][j]

            if value == target:
                return True

            if value > target:
                tail = mid - 1

            if value < target:
                head = mid + 1

        return matrix[head  // size_j][head % size_j] == target

Complexity Analysis

• Time Complexity: O(log(n)), as for a binary search algorithm, wheres n indicates numbers of elements in the 2D-array here.
• Space Complexity: O(1), as only constant variable is involved.