872. Leaf-Similar Trees

Problem

Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a leaf value sequence.

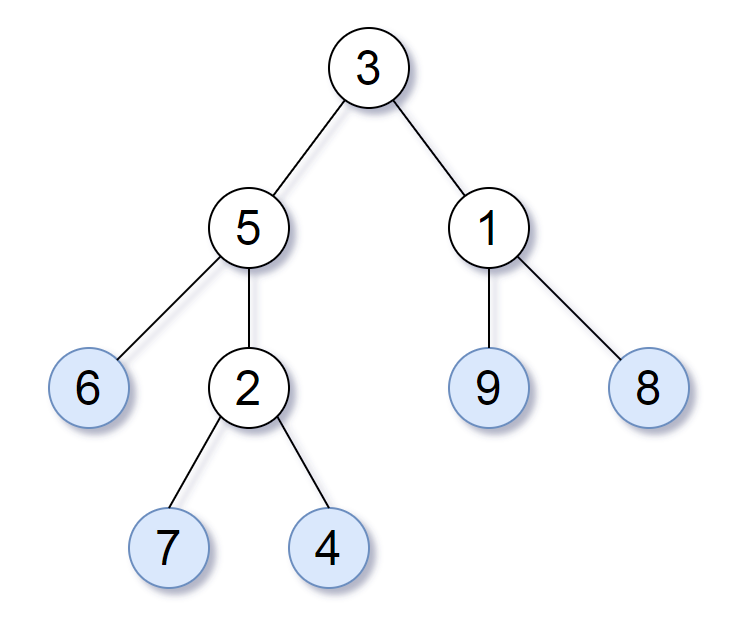
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

Example 1:

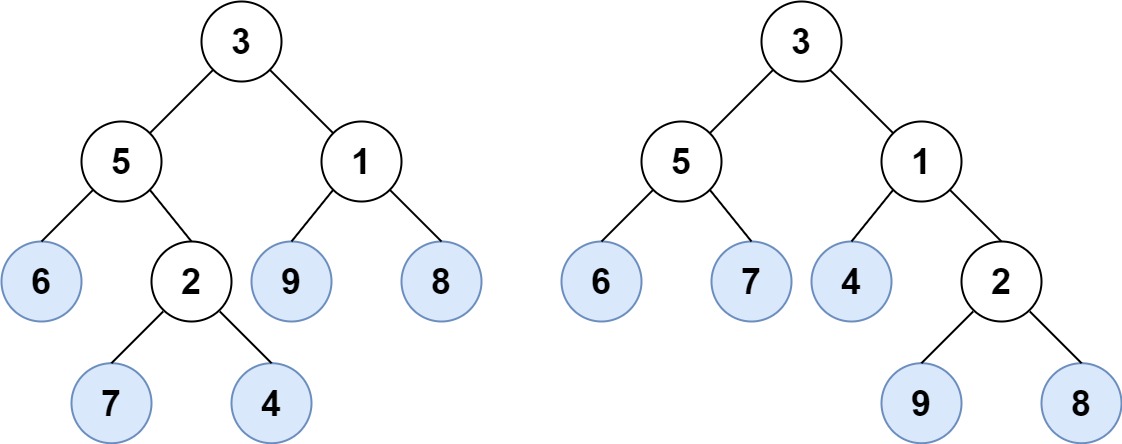
Input: root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
Output: true

Example 2:

Input: root1 = [1], root2 = [1]
Output: true

Example 3:

Input: root1 = [1], root2 = [2]
Output: false

Example 4:

Input: root1 = [1,2], root2 = [2,2]
Output: true

Example 5:

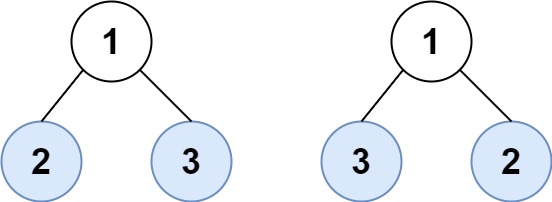
Input: root1 = [1,2,3], root2 = [1,3,2]
Output: false

Constraints:

• The number of nodes in each tree will be in the range [1, 200].
• Both of the given trees will have values in the range [0, 200].

Discussion

The problem requires us to find compare two trees with the sequence of their leaf nodes. As the leaf nodes may not by lying on the same level, we are going to use DFS to scan for the leaf nodes as array and perform comparison.

Solution

Our solution starts with writing an standard DFS function to scan for leaf nodes. Leaf nodes are then appended to target array. A complete DFS function should scan all the leaf nodes and put them to an array with maintained sequence.

We simply compare the two array and result is obtained.

class Solution:
    def leafSimilar(self, root1: TreeNode, root2: TreeNode) -> bool:
        self.arr = []

        self.dfs(root1)
        arr1, self.arr = self.arr, []

        self.dfs(root2)
        arr2, self.arr = self.arr, []

        return arr1 == arr2

    def dfs(self, root):
        if not root:
            return
        if root.left:
            self.dfs(root.left)
        if not root.left and not root.right:
            self.arr += [root.val]
        if root.right:
            self.dfs(root.right)

Complexity Analysis

• Time Complexity: O(n), as DFS scan all the nodes in a tree and giving a linear time complexity. Perform it twice gives an linear solution as well.
• Space Complexity: O(n), regardless of the deep recursion memory for DFS, we are caching all the leaf nodes in a array, which causing linear space complexity already.